Produtos notáveis
Quadrado da soma de dois termos
O quadrado da soma de dois termos a e b é indicado por ( a + b )²
Para calculá-lo, basta multiplicar a + b por a + b:
( a + b )² = ( a + b ) ( a + b )
( a + b )² = a.a + a.b + b.a + b.b
( a + b )² = a² + a.b + b.a + b²
Como a.b = b.a vem que
( a + b )² = a² + 2ab + b²
quadrado duas vezes quadrado
do o produto do
1º termo dos termos 2º termo
O quadrado da soma de dois termos é igual ao quadrado do primeiro, mais duas vezes o produto do primeiro pelo segundo, mais o quadrado do segundo termo.
Exemplos:
( x + 3 )² = x² + 2.x.3 + 3² = x² + 6x + 9
( 2x + 1)² = (2x)² + 2.2x.1 + 1² = 4x² + 4x + 1
(5x + 3y)² = (5x)² + 2.5x.3y + (3y)² = 25x² + 30xy + 9y²
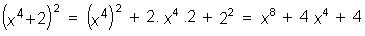
Calcule:
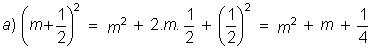
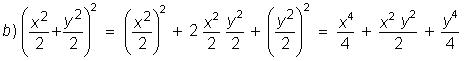
c) (x + 1)² + (x + 2)² - (2x + 1)² = [x² + 2x + 1] + [x² + 4x + 4] – [4x² + 4x + 1] =
= x² + 2x +1 + x² + 4x + 4 – 4x² - 4x – 1 =
= -2x² + 2x + 4
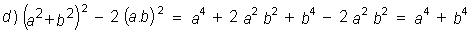
e) (x + 1).(x + 2) – 2.(x + 2)² + (x + 2).(x + 3) =
= x² + 2x + x + 2 – 2[x² + 4x + 4] + x² + 3x + 2x + 6 =
= x² + 2x + x + 2 – 2x² - 8x – 8 + x² + 3x + 2x + 6 = 0
Quadrado da diferença de dois termos
O quadrado da diferença entre dois termos a e b é indicado por (a – b)²
Para calculá-lo basta multiplicar a – b por a – b:
(a – b)² = (a – b)(a – b)
(a – b)² = a² - ab – ba + b²
(a – b)² = a² - 2ab + b²
O quadrado da diferença entre dois termos é igual ao quadrado do primeiro, menos duas vezes o produto do primeiro pelo segundo, mais o quadrado do segundo termo.
Exemplos:
(x – 3)² = x² - 2.x.3 + 3² = x² - 6x + 9
(2x – 1)² = (2x)² - 2.2x.1 + 1² = 4x² - 4x + 1
(5x – 3y)² = (5x)² - 2.5x.3y + (3y)² = 25x² - 30xy + 9y²


